The thirteen-sided hat was cool for a hot second, but the new and improved einstein tile, Spectre, has taken its place. If you don't know what I'm talking about, it's ok. I've only just learned about this takeover myself. I am referring to the recent discovery in aperiodic tiling. More on what that is in a minute.
First, let's talk about the tiling we all know - periodic tiling (or simply, tiling). Tiling is a shape or set of shapes that creates a bigger pattern and it repeats over and over. You've seen this kind everywhere - on floors, walls, and decorations. Like this design that I found on the wall of a bathroom in Berlin:
So, aperiodic tiling is a shape or set of shapes that fit together with no spaces and covers a surface entirely, without creating a repeating pattern. It's a puzzle that has been holding the attention of math enthusiasts since at least 1964, when Robert Berger discovered the first aperiodic tiling consisting of 20,426 distinct tiles. And, to very quickly summarize decades of work through numerous mathematicians, that number has dramatically decreased all the way to one. And in March 2023 this one tile, which resembles a hat, was named the "einstein", meaning "one stone" in German.
Here is the hat:
The hat tile: David Smith, Joseph Samuel Myers, Craig S. Kaplan, and Chaim Goodman-Strauss via Scientific American
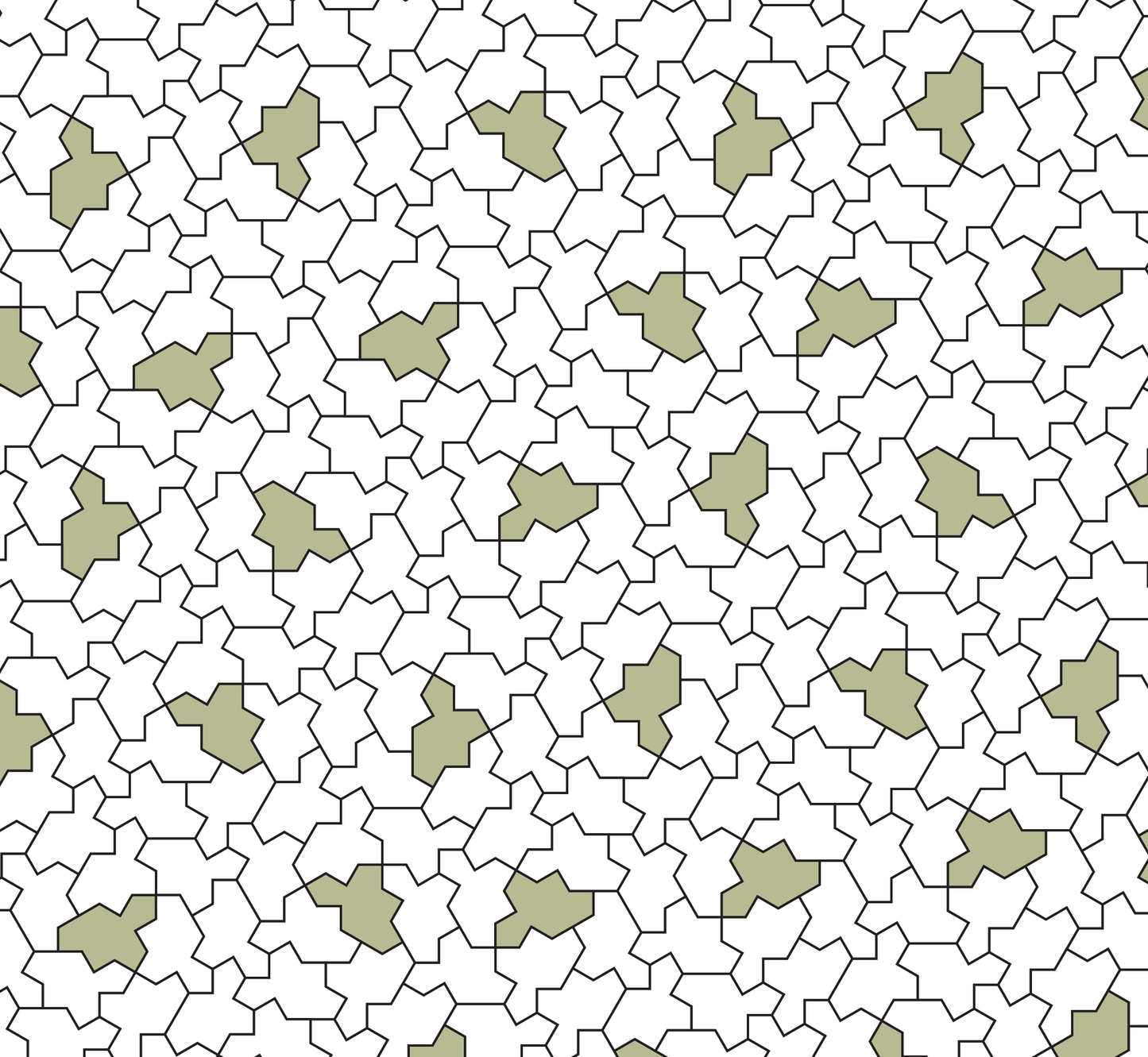
Impressive! Until we realize that the einstein hat had to be flipped over in a few spots to cover the surface, which technically could be considered a second shape. So the team tweaked the design until they did not have to use mirror-images of the shape. This brings us to Spectre:
Spectre tile: David Smith, Joseph Samuel Myers, Craig S. Kaplan, and Chaim Goodman-Strauss via A Chiral Aperiodic Monotile
So, is that it? Problem solved? We did it? I guess so, unless another imperfection is discovered. That's the end of the einstein tile as we know it - the beautiful conclusion of 60 years of working on a puzzle.
For a thorough technical explanation, read the original white paper:
.
References
Bischoff, M 2023, 'Newfound Mathematical "Einstein" Shape Creates a Never Repeating Pattern', Scientific American, 10 April, accessed August 2023, <https://www.scientificamerican.com/article/newfound-mathematical-einstein-shape-creates-a-never-repeating-pattern/>
McFadden, C 2023, 'Forget the 'Einstein' Tile, Meet the True Aperiodic Tile "Spectre"', Interesting Engineering, 4 June, accessed August 2023, <https://interestingengineering.com/innovation/einstein-true-aperiodic-tile-spectre>